Relations de conjugaison – Philippe Lenepveu

Relations de Descartes et de Newton, formules.

Définitions

Relation de conjugaison (ou formule de conjugaison) : formule mathématique reliant la position d’un objet à celle de son image par un système optique.

o: Dimension de l’objet.
i: Dimension de l’image.
p: Distance de l’objet au centre optique.
x: Distance de l’objet au point focal objet.
f: Distance focale objet.
f’: Distance focale image.
x′: Allongement, ou distance du point focal image à l’image.
p’: Tirage, ou distance du centre optique à l’image.
D: Distance de l’objet à l’image (p+p’).

N.B. : la distance focale objet est égale à la distance focale image (f = f’).

Relation de Descartes

Relation de Descartes : relation de conjugaison avec origine aux points principaux.

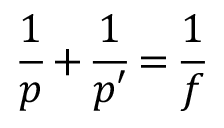
1∕p + 1∕p' = 1∕f

Relation de Newton

Relation de Newton : relation de conjugaison avec origine aux foyers.

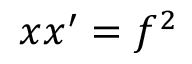
x·x' = f²

Grandissement

Par définition, le grandissement est égal à la dimension de l’image sur la dimension de l’objet (g = i / o). On a les relations suivantes :

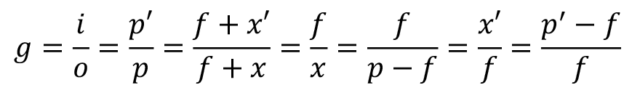
g = i∕o
g = p'∕p
g = (f+x')/(f+x)
g = f∕x
g = f ∕ (p-f)
g = x'∕f
g = (p'-f) ∕ f

Exemples de calculs

Connaissant la focale et le grandissement, on obtient :

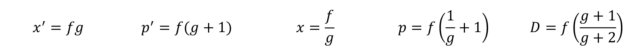
x' = f×g
p' = f×(g+1)
x  = f∕g
p  = f×(1∕g+1)
D  = f×(g+1∕g+2)

Exemple : soit un objectif de 50 mm de distance focale. Pour un grandissement de 1 (dimension de l’image = dimension de l’objet), on a :

tirage x’ = 50 mm
allongement p’ = 100 mm
distance D de l’objet à l’image = 200 mm

Pour un grandissement de 0,1 (image 10 fois plus petite que l’objet), on a :

tirage x’ = 5 mm
allongement p’ = 55 mm
distance D de l’objet à l’image = 605 mm

Connaissant le grandissement et la distance de l’objet au centre optique, on obtient :

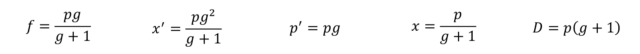
f  = p×g∕(g+1)
x' = p×g²∕(g+1)
p' = p×g
x  = p∕(g+1)
D  = p×(g+1)

Connaissant la focale et le tirage, on obtient :

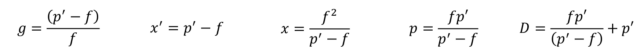
g  = (p'-f)/f
x' = p'-f
x  = f²/(p'-f)
p  = f×p'/(p'-f)
D  = f×p'/(p'-f)+p’

Connaissant la focale et l’allongement, on obtient :

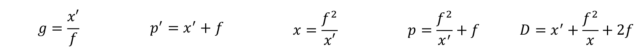
g  = x'∕f
p' = x' + f
x  = f²∕x'
p  = f²∕x' + f
D  = x' + f²∕x' + 2×f

Exemple : soit un objectif de 50 mm de distance focale. Pour un allongement x’ de 1 mm, la distance D de l’objet à l’image est égale à 2,60 m environ.

Connaissant la focale et la distance de l’objet au plan focal objet, on obtient :

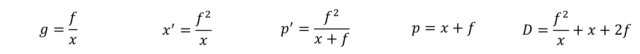
g  = f∕x
x' = f²∕x
p' = f²∕x + f
p  = x + f
D  = f²∕x + x + 2×f

Connaissant la focale et la distance de l’objet au centre optique, on obtient :

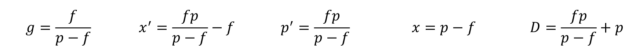
g  = f/(p-f)
x' = f×p∕(p-f) - f
p' = f×p∕(p-f)
x  = p - f
D  = f×p∕(p-f)+p

Connaissant la focale et la distance de l’objet à l’image, on obtient :

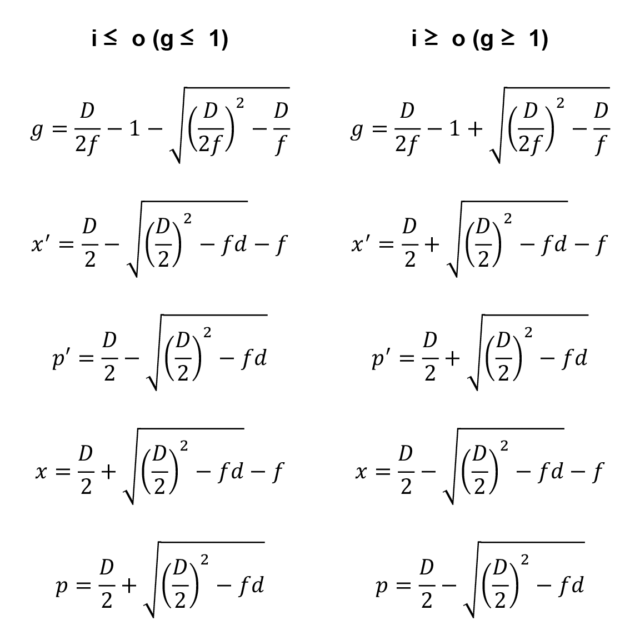
Pour i ≤ o (g ≤ 1) :

g  = D∕(2×f) - 1 - √((D∕(2×f))² - D∕f)
x' = D∕2 - √((D∕2)² - f×D) - f
p' = D∕2 - √((D∕2)² - f×D)
x  = D∕2 + √((D∕2)² - f×D) - f
p  = D∕2 + √((D∕2)² - f×D)

Pour i ≥ o (g ≥ 1) :

g  = D∕(2×f) - 1 + √((D∕(2×f))² - D∕f)
x' = D∕2 + √((D∕2)² - f×D) - f
p' = D∕2 + √((D∕2)² - f×D)
x  = D∕2 - √((D∕2)² - f×D) - f
p  = D∕2 - √((D∕2)² - f×D)

Exemple : soit un objectif de 50 mm de distance focale. Dans le cas d’une image plus petite que l’objet (g < 1), pour une distance de mise au point de 5 m, l’allongement x’ est égal à 0,51 mm environ.